Convolutional Neural Networks

A convolutional neural network, or CNN for short, is specifically designed to process pixel and image data, which is why it excels at image recognition tasks such as the mask classifier. They do this using an operation called a convolution, which is applied to the image in a convolution layer. When a convolution is applied to an image, the model slides many learnable filters, or kernels, across the image. These kernels are much smaller than the image; for example, the image might be 128 pixels by 128 pixels, while the kernel is only 3 pixels by 3 pixels. Each of the pixels in the kernel has an activation value that is multiplied by the subset of the image that the kernel is over. These multiples are then summed and used to create a new, smaller image.

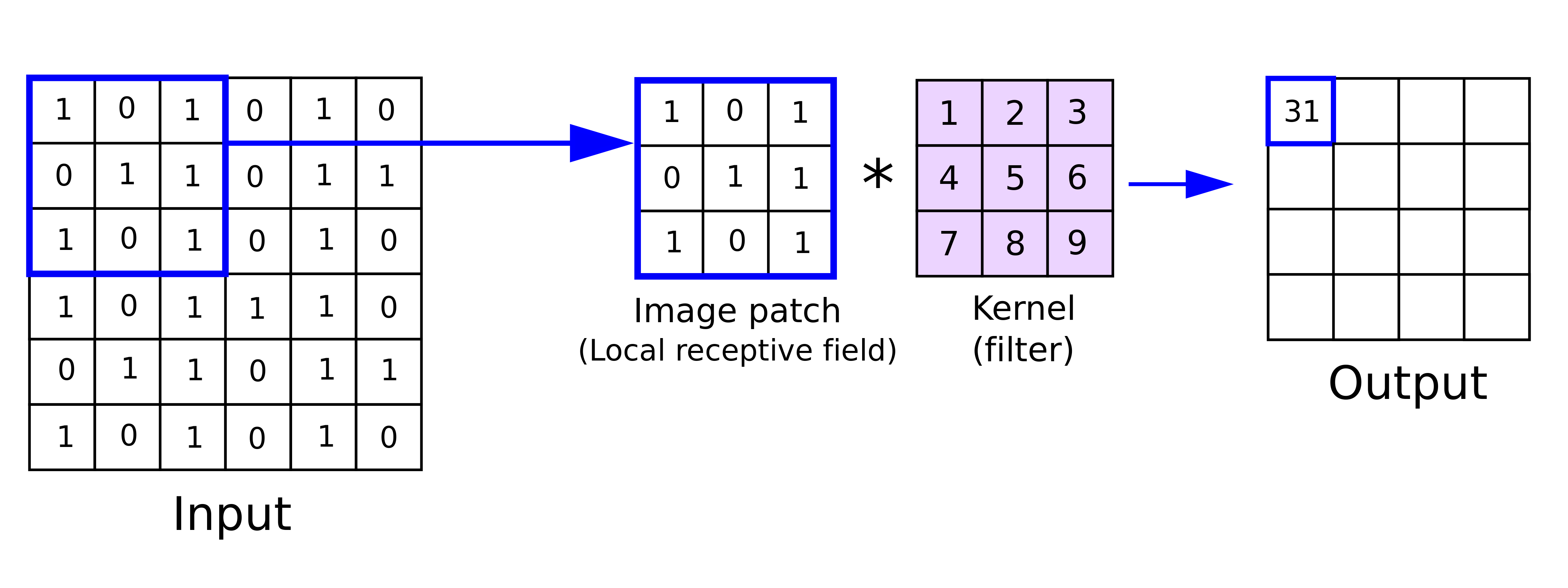The 3x3 kernel is applied to the 6x6 image; In this case, the output is 1+3+5+6+7+9=31

The genius of convolutions is that they mimic human vision, specifically feature detectors, and how incredibly responsive we are to patterns in information.

Max-pooling is applied to a 8 x 8 image to produce a 2 x 2 image

Still, besides convolutional layers, there are also max-pooling layers. Max-pooling layers also have a kernel that slides across the image, but the smaller image they generate is composed of the largest values of each of the frames. On top of this,

• Strides define how far each filter moves in between the locations it is applied
• Max pooling essentially summarizes an image. The model can either learn to make important parts of the image have higher values or naturally prefer brighter parts of the image, which usually provide more information
• Activation functions are applied before max pooling. Briefly, activation functions both normalize and add complexity to the output of a neuron. For example, the ReLU (Rectified Linear Unit) activation function replaces negative values with 0 through the function $ReLU(x) = max(0,x)$

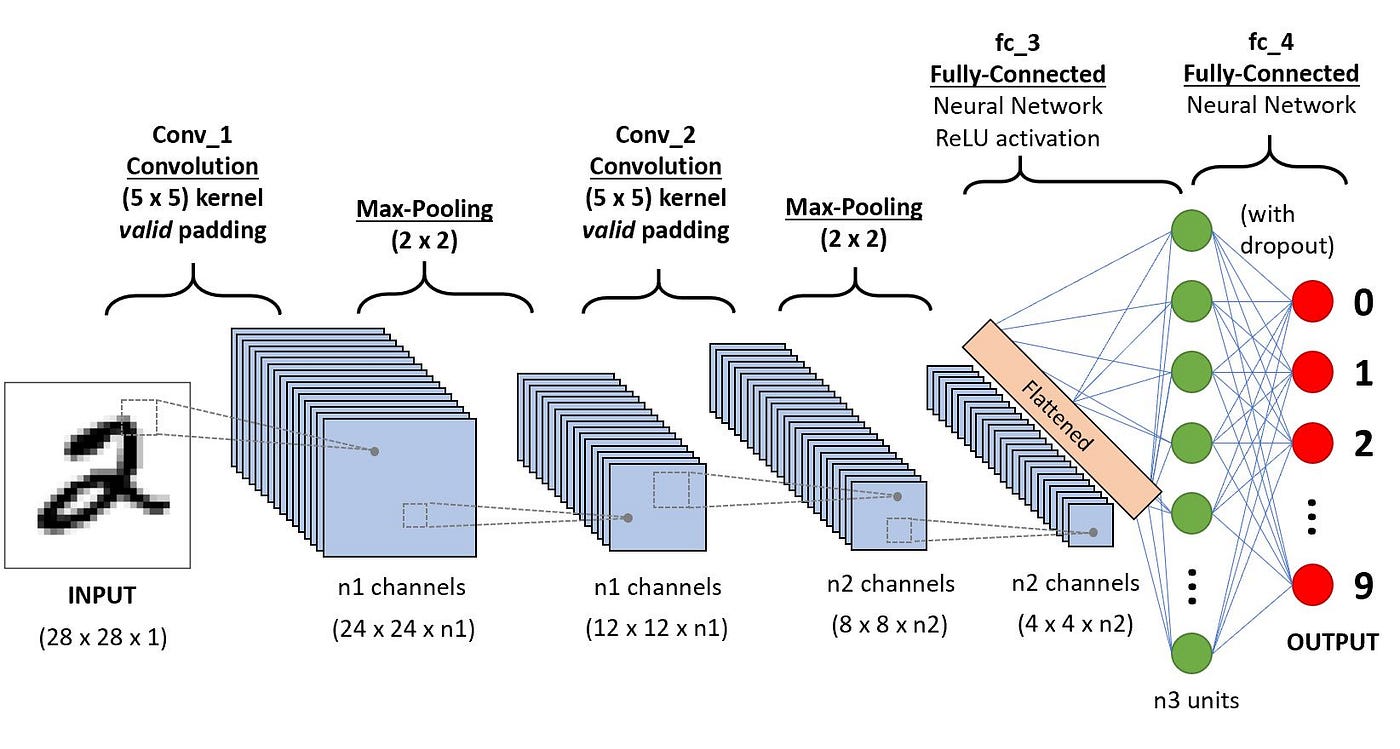
Now, hopefully you can try to understand this image!

• The size of the output of Conv_1 is (24 x 24 x # of filters, or n1)
• Ignore the Fully-Connected layers, more about them can be found here
• When the last Max-Pooling layer is flattened, the (4 x 4 x n2) layer is transformed into a ((4 * 4 * n2) x 1) layer, compressing the data into 1-dimensional array

Here’s a simpler diagram. Note that it does not show how multiple filters are being applied. The convolution also does not necessarily force the model to “look” at only a portion of the image, although it may encourage this through its filters.

CNNs are proven to be better for image classification and related tasks compared to other models. Here’s how one might implement a CNN in TensorFlow.

model = tf.keras.Sequential([
	tf.keras.layers.Conv2D(32, (3,3), padding='same', activation=tf.nn.relu,
		input_shape=(28, 28, 1)),
	tf.keras.layers.MaxPooling2D((2, 2), strides=2),
	tf.keras.layers.Conv2D(64, (3,3), padding='same', activation=tf.nn.relu),
	tf.keras.layers.MaxPooling2D((2, 2), strides=2),
	tf.keras.layers.Flatten(),
	tf.keras.layers.Dense(128, activation=tf.nn.relu),
	tf.keras.layers.Dense(10, activation=tf.nn.softmax)
])

The two last layers are the fully connected “normal” neural network layers. There are 128 nodes of fully connected neurons, which means that each of the nodes is connected to each flattened neuron, followed by 10 neurons in the output layer. This model was made for classifying the MNIST handwritten digits dataset, so there are 10 classes for 10 digits, and they have a softmax activation so that the output represents a probability (the sum of the outputs is 1).

Obviously, the amount of output neurons for a CNN changes based on the task. For example, in a binary (two-class) classification problem, the output layer would be one neuron, representing the probability of the input being one of the classes. This would use the sigmoid activation function.

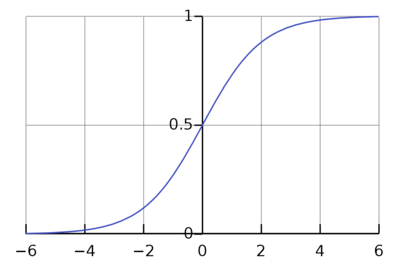
The sigmoid activation function $σ(x) = \frac{1}{1+e^{-x}}$